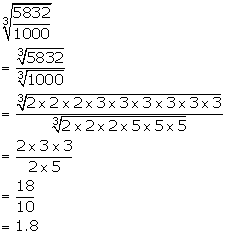Find The Square Root Of 5832

Also tells you if the entered number is a perfect square.
Find the square root of 5832. Let us say n is the value of 3 729 then n n n n 3 729. If you have been looking for square root of five thousand eight hundred and thirty two then you are right here too on this page you can also find what the parts of 5832 are called and in addition to the terminology of. Square root calculator and perfect square calculator. Simplified square root for 5832 is 54 2.
Let s check this width 324 1 5832. Now extract and take out the cube root 324 1. B hence find the square root of 324. A express 225 as a product of its prime factors.
A perfect square root is any square root that s a whole number. The square root of 5832 is the number which multiplied by itself is 5832. Do this by testing perfect squares until you get to a number whose square if greater that 529 for example 25 2 625 so we test 2 2 4. This is the usual definition of the cube root of a number.
Check for divisibility by a perfect square to simplify. The square root of a number is really easy to find. Clearly 4 is not a factor of 529 nor is any other even number. 5832 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3 2 x 3 x 3 3 5832 2 x 3 x 3 18 if you truly did want the square root then it would be.
You will find that 23 2 529 when we try to simplify a square root we look for perfect square factors. The cube root of 729 denoted as 3 729 is a value which after getting multiplied by itself thrice gives the original value. 5832 has the square factor of 2916. 5832 has the cube factor of 324.
First we will find all factors under the cube root. A express 3969 as a product of its prime factors. Calculate the positive principal root and negative root of positive real numbers. 5832 2 x 3 x 3 x 3 x 2 5832 2 x 3 x 3 x 3 x 2 x 54 2 76 367532368.
To calculate a square root by hand first estimate the answer by finding the 2 perfect square roots that the number is between. As you can see the radicals are not in their simplest form. B hence evaluate 9. Let s remember first that finding the square root of a number is the opposite of finding the exponent of a number.
For example if you re trying to find the square root of 7 first you d need to find the first perfect square below 7 which is 4 and the first perfect. Step by step simplification process to get square roots radical form. Find the square root or the two roots including the principal root of positive and negative real numbers. First we will find all factors under the square root.
In other words the square of this number equals five thousand eight hundred and thirty two. By expressing 5832 as the product of its prime factors find its cube root. Cube of 324 18 which results into 18 1. Moreover we are only going to deal with positive square roots a negative square root will result on imaginary numbers.
Since 729 is a perfect cube we will use the prime factorisation method to get the cube root easily. All radicals are now simplified.