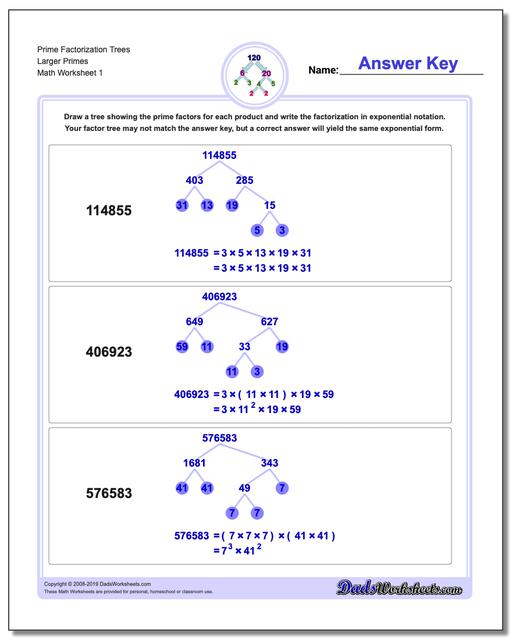
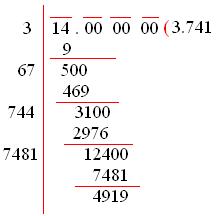Find The Square Root Of 1681 By Prime Factorization Method

Finding the square root by prime factorization method.

Find the square root of 1681 by prime factorization method. Https bit ly exponentsandpowersg8 in this video we will learn. Prime factorization by trial division. Generally prime factorization is used for finding square roots of small numbers. Say you want to find the prime factors of 100 using trial division.

Square root by prime factorization method example 1 find the square root. To learn more about squares and square roots enrol in our full course now. Finding cube root by prime factorization. We cover two methods of prime factorization.

Find primes by trial division and use primes to create a prime factors tree. 0 00 how to fin. Resolve it into prime factors. Iii combine the like square root terms using mathematical operations.

E learning is the future today. Ii inside the square root for every two same numbers multiplied one number can be taken out of the square root. Ex 6 3 4 find the square roots of the following numbers by the prime factorization method. We can find square root by prime factorization method or by long division method.

Take one factor from each pair. Covid 19 has led the world to go through a phenomenal transition. Obtain the given number. Finding square root of a number by prime factorization square root of a number is the value that returns the original number on multiplied by itself.

Finding square root by prime factorisation is an easy method. I 729we use prime factorization to find square root thus 729 3 3 3 3 3 3square root of 729 3 3 3 9 3 27 ex 6 3 4 find the square roots of t. Stay home stay safe and keep learning. Find the product of factors obtained in step iv.

Thew following steps will be useful to find square root of a number by prime factorization. Start by testing each integer to see if and how often it divides 100 and the subsequent quotients evenly. I decompose the number inside the square root into prime factors. Since the number is a perfect square you will be able to make an exact number of pairs of prime factors.