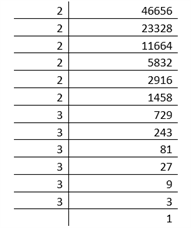
Find The Square Root Of 11664 By Prime Factorisation Method

The prime factors of 8100 is.

Find the square root of 11664 by prime factorisation method. It is often taken as the smallest natural number however some authors include the natural numbers from zero. The square root of 8100 is 90. Thew following steps will be useful to find square root of a number by prime factorization. Create sieve of erasthones for the.

Https bit ly exponentsandpowersg8 in this video we will learn. Hence the square root of 8100 is 90. Since the number is a perfect square you will be able to make an exact number of pairs of prime factors. Click here to get an answer to your question find the square root of a number 7744 by prime factorisation method.

Iii combine the like square root terms using mathematical operations. To find square root we have to write one number for each pair. Cubed root of 11664. Find the product of factors obtained in step iv.

Your prime factorization is the empty product with 0 factors which is defined as having a value. We can find square root by prime factorization method or by long division method. Calculating the prime factorization of large numbers is not easy but the calculator can handle pretty darn big ones determine whether or not a number is prime. This is a step by step guide for finding the value of square root of 4096 for finding the square root of any number we have two methods.

Generally prime factorization is used for finding square roots of small numbers. We have to find the square root of above number by prime factorization method. Find the square root of a n. Prime factors of 11664.

Square root by prime factorization method example 1 find the square root. Calculate the prime factorization of the number you type numbers above 10 million may or may not time out. The prime factorization calculator can. The product obtained in step v is the required square root.

So in any factorization of n at least one of the factors must be smaller than the square root of n and if we can t find any factors less than or equal to the square root n must be a prime. 0 00 how to fin. The number 1 is not a prime number but a divider for every natural number. Take one factor from each pair.

Now a and b can t be both greater than the square root of n since then the product a b would be greater than sqrt n sqrt n n. Given the number 8100. To learn more about squares and square roots enrol in our full course now. Squares and square roots.