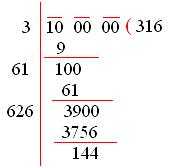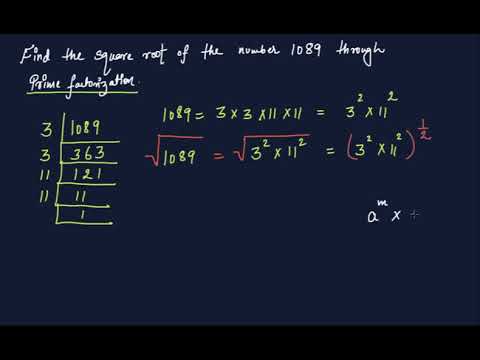Find The Square Root Of 1056 25 By Division Method

Let us understand long division method with the help of an example.

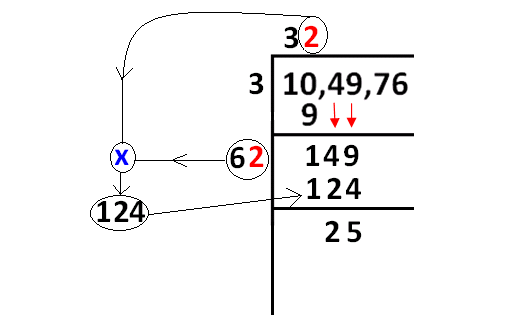
Find the square root of 1056 25 by division method. Ex 6 4 1 find the square root of each of the following numbers by division method. The following is the stepwise solution for this method. Calculate square root of 5 using division method. For digits after decimal point pair them from left to right.

Remainder when 17 power 23 is divided by 16. Another method to find the square root of any numbers is long division method. Thus we have 05. Finding square root using long division.

Sum of all three digit numbers divisible by 6. Find the square root of 625. Divide the digits of the number into pairs of segments starting with the digit in the units place. Pairing the numbers to get the perfect squares we get.

Translating the word problems in to algebraic expressions. Square root of a number by long division method. Online calculator which calculates the square root of a given number using long division ld method. Let us see some examples here.

Place a bar over every pair of digits starting from the unit digit. Long division is a very common method to find the square root of a number. L c m method to solve time and work problems. Sum of all three digit numbers divisible by 7.

Also to find the square roots of imperfect squares such as 2 3 5 6 8 etc we can use long division method avoiding the use of calculators. Here s a link of how to find square root of irrational numbers by division method in hindi https www yout. 625 25 x 25 25 2. How to find square root using long division method.

Perform division as per steps shown below. Group the digits into pairs for digits to the left of the decimal point pair them from right to left. 625 5 x 5 x 5 x 5. I 2304 thus square root of 2304 48let s look at individual steps as well individual steps are explainedstep 1 write the numberwe make pairs from right so 04 and 23 are two pairs.

Learn to find the square root by division method. Remainder when 2 power 256 is divided by 17. Hence 625 25. The following is the stepwise solution for this method.

By prime factorisation we know. Taking 484 as the number whose square root is to be evaluated.